Can you imagine such a short code solving the 24-point game?

The 24 Point Game is a classic puzzle game played with playing cards. The rules of the game are as follows: Remove the Jokers from a deck of playing cards, leaving 52 cards, randomly draw 4 cards, and use the numbers on the cards (where J, Q, K, A represent 11, 12, 13, 1 respectively) in combination with addition, subtraction, multiplication, division, and parentheses to achieve a result of 24. Each card must be used once and only once.

Write code to calculate 24 for any given four cards, outputting the solution in text format.

try.DEMO

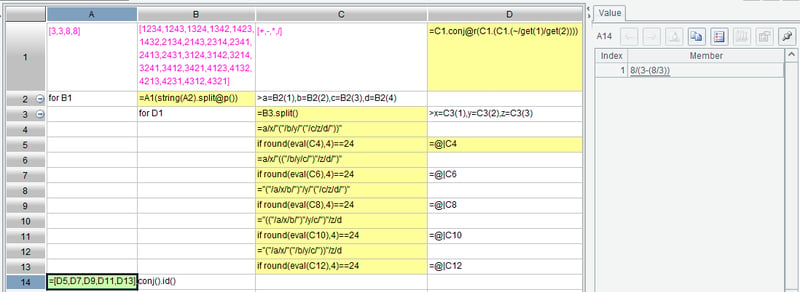
A1 sets the four cards to be used for calculation, B1 enumerates all possible permutations for the four cards, and C1 lists the available arithmetic operators.

Since three operators need to be placed between the four cards, and each can be chosen arbitrarily, D1 utilizes multi-layer loops to list all possible operator combinations. In SPL, the A.conj@r() function, when used at the outermost loop, can union all the results of all layers to a sequence. The results in D1 are as follows:

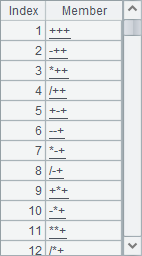
If you don’t want to manually write the enumeration results in B1, you can generate them using an expression: =4.conj@r(4.(4.(4.([~,get(1),get(2),get(3)]).select(~.icount()==4).(~.concat())))). Unlike C1, this requires selecting permutations that use all four cards, with each card used exactly once.

A2 loops through each permutation of the cards. B2, based on that permutation, retrieves the four numbers needed to calculate 24. For convenience, C2 assigns the four numbers to virables a, b, c, and d.

B3 loops through each available operator for every group of numbers. C3 splits the operators into a sequence. D3 assigns each operator to the vairables x, y, and z respectively.

Given a combination of numbers and operators in the form a#b#c#d, there are five distinct orders of operations that can be expressed using parentheses: a#(b#(c#d)), a#((b#c)#d), (a#b)#(c#d), ((a#b)#c)#d, and (a#(b#c))#d.

Within the loop, try each of the five operation orders in sequence. For example, C4 constructs the expression for the operation order a#(b#(c#d)), and C5 uses eval to calculate the result of that expression. To avoid the effects of calculation errors, the results need to be rounded using the round function, keeping 4 decimal places here. If the result of the expression is exactly 24, it indicates the expression in C4 satisfies the requirement. In this case, record the result in D5. Similarly, C6, C8, C10, and C12 construct expressions for the other four operation orders, and expressions that evaluate to 24 are then recorded in D7, D9, D11, and D13 respectively.

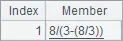
Once the loop ends, A14 retrieves all the expressions that meet the requirement and concatenates them to a sequence using conj. Because the given cards might be repeated, identical expressions may exist in the results, and therefore deduplication using id is necessary. A14’s output is as follows:

In the above solution, when analyzing the five operation orders for a given combination of numbers and operators, similar processing and checks were actually performed. This can be further simplified using a loop, as shown below:

try.DEMO

A2 prepares to store the results, and B2 lists the expressions corresponding to the five operation orders, where each variable is represented by ?. Inside the loop, when C5 evaluates a given number and operator combination, it iterates through each operation order in B2. The eval(s, x1,x2,…) function can sequentially replace ? in the string s with the values of x1,x2, and so on. Here, by inputting the numbers and operators into the parameter list in the required order, the corresponding expression exp can be obtained. Using eval again, the result of the expression can be calculated, and if the result is 24, the expression is recorded in A2.

esProc SPL is open-sourced and now available here if you are interested in it: Open-Source Address.